Giải hệ phương trình - Biến arduino thành máy tính

Bạn có bao giờ nghĩ thuật toán để tìm nghiệm của hệ phương trình là gì trong các máy tính cầm tay  ? Bài viết này sẽ trình bày cho các bạn một phương pháp tổng quát và cụ thể nhất đó là tính định thức ma trận vuông cấp n. Với phương pháp này các bạn có thể giải hệ phương trình n ẩn tùy ý miễn là arduino của các bạn đủ dung lượng SRAM và bộ nhớ flash. Không dài dòng nữa vào vấn đề chính thôi nào.

Yêu cầu

Có kiến thức và đam mê về lập trình arduino và Toán Học. Vì bài viết này sẽ không cần đấu nối điện tử gì cả, nhưng kiến thức về ma trận có thể làm "rớt não" và là ác mộng của sinh viên đại học . Và một ít kiến thức về dùng máy tính giao tiếp với arduino thông qua serial bằng cách làm thủ công và không dùng thư viện Serial Command. Mình vẫn còn là học sinh THPT nên nếu có kiến thức nào về ma trận không thỏa đáng thì xin các cao nhân thứ cho và chỉ giáo ạ .

Ý tưởng

Chúng ta sẽ đi từ dễ đến khó trước. Giả sử ta có một hệ phương trình hai ẩn như sau:

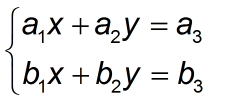
Để tìm nghiệm tổng quát ta cần tìm 3 định thức ma trận 2x2 sau:

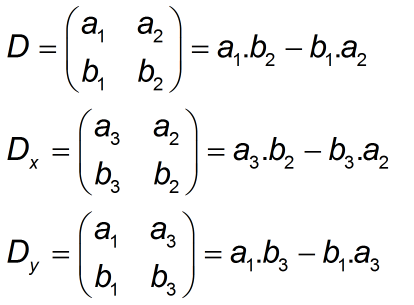
Từ đó ta có công thức nghiệm tổng quát của hệ là (nếu det D=det D_x= det D_y=0 thì hệ có vô số nghiệm còn nếu det D=0 và det D_x, det D_y khác 0 thì hệ vô nghiệm):

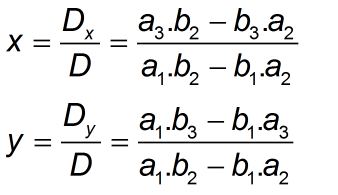
Tương tự như vậy giả sử ta có một hệ phương trình 3 ẩn:

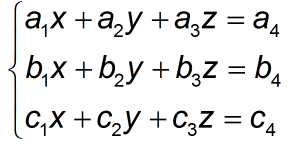
Ta cần tính 4 định thức ma trận vuông 3x3 như sau:

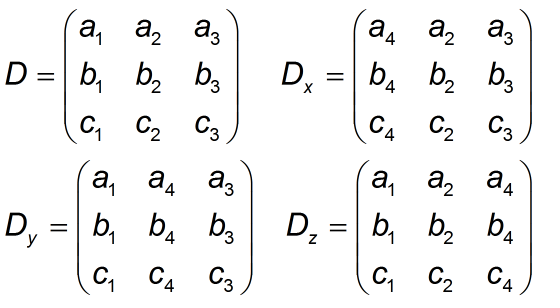
Ta sẽ tính định thức ma trận 3x3 bằng cách khai triển theo hàng. Xét ma trận 3x3 tổng quát thế thì định thức của nó là:

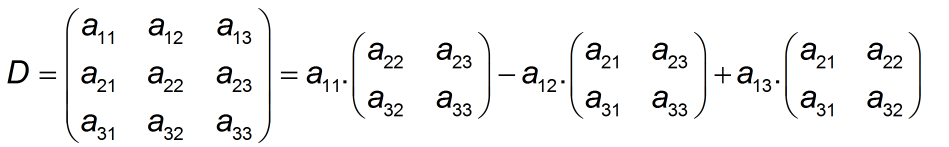
Và một lần nữa ta thu được nghiệm tổng quát của phương trình là:

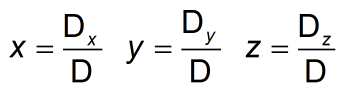
Từ đó, với ý tưởng tạo ra một hàm tính định thức ma trận 2x2 thì ta có thể lồng ghép các hàm lại với nhau để tính ma trận nxn. Ví dụ để tính ma trận 4x4 ta cần hàm tính ma trận 3x3, và để tính ma trận 3x3 ta cần hàm tính ma trận 2x2, thật đơn giản phải không nào .

Lập trình

Các bạn nạp đoạn code sau vào arduino, bật Serial Monitor và nhập giá trị các biến.

String input;
char bien[]={'a','b','c','d','e','f','g','h','i','k','l','m'};
float variable[13]={};
float x;
float y;
float z;
void setup() {
Serial.begin(9600);
Serial.println("System of equations Caculator");
}

void loop(){
Serial.println("Type variable's quantities");
while(Serial.available()==0){}
  if(Serial.available()>0){
  input =Serial.readStringUntil('\n');
  if(input == "2"){Serial.println("2 variables equation"); nhapheso2an();}
  if(input == "3"){Serial.println("3 variables equation"); nhapheso3an();}
  }
}
void nhapheso2an(){
Serial.println("ax+by=c");
Serial.println("dx+ey=f");
byte count=1;
byte i;
byte m;
while(count<7){
for (i=1; i<7; i++){if(count==i){m=i; Serial.print("Type value of "); Serial.println(bien[i-1]);}}
while(Serial.available()==0){}
  if(Serial.available()>0){
  input =Serial.readStringUntil('\n');
  variable[m-1]=input.toFloat();
  count++;
  }}
giaihe2an();
delay(500);
}
void nhapheso3an(){
Serial.println("ax+by+cz=d");
Serial.println("ex+fy+gz=h");
Serial.println("ix+ky+lz=m");
byte count=1;
byte i;
byte m;
while(count<13){
for (i=1; i<13; i++){if(count==i){m=i; Serial.print("Type value of "); Serial.println(bien[i-1]);}}
while(Serial.available()==0){}
  if(Serial.available()>0){
  input =Serial.readStringUntil('\n');
  variable[m-1]=input.toFloat();
  count++;
  }}
giaihe3an();
delay(500);
}
void giaihe2an(){
float det;
float detx;
float dety;
det= matrix2(variable[0],variable[1],variable[3],variable[4]);
detx= matrix2(variable[2],variable[1],variable[5],variable[4]);
dety= matrix2(variable[0],variable[2],variable[3],variable[5]);
if((det==0)&&(detx==0)&&(dety==0)){Serial.println("Infinite Solution");}else{if(det==0){Serial.println("No Solution");}
else{
Serial.print("x = ");
Serial.print(detx);
Serial.print("/");
Serial.print(det);
Serial.print(" = ");
Serial.println(detx/det, 15);
Serial.print("y = ");
Serial.print(dety);
Serial.print("/");
Serial.print(det);
Serial.print(" = ");
Serial.println(dety/det, 15);
}}
}
void giaihe3an(){
float det;
float detx;
float dety;
float detz;
det= matrix3(variable[0],variable[1],variable[2],variable[4],variable[5],variable[6],variable[8],variable[9],variable[10]);
detx= matrix3(variable[3],variable[1],variable[2],variable[7],variable[5],variable[6],variable[11],variable[9],variable[10]);
dety= matrix3(variable[0],variable[3],variable[2],variable[4],variable[7],variable[6],variable[8],variable[11],variable[10]);
detz= matrix3(variable[0],variable[1],variable[3],variable[4],variable[5],variable[7],variable[8],variable[9],variable[11]);
if((det==0)&&(detx==0)&&(dety==0)&&(detz==0)){Serial.println("Infinite Solution");}else{if(det==0){Serial.println("No Solution");}
else{
Serial.print("x = ");
Serial.print(detx);
Serial.print("/");
Serial.print(det);
Serial.print(" = ");
Serial.println(detx/det, 15);
Serial.print("y = ");
Serial.print(dety);
Serial.print("/");
Serial.print(det);
Serial.print(" = ");
Serial.println(dety/det, 15);
Serial.print("z = ");
Serial.print(detz);
Serial.print("/");
Serial.print(det);
Serial.print(" = ");
Serial.println(detz/det, 15);
}}
}
float matrix2(float a, float b, float c, float e){
float det = a*e-b*c;
return det;
}
float matrix3(float a,float b,float c,float e,float f,float g,float h,float i,float k){
float det = a*matrix2(f,g,i,k)-b*matrix2(e,g,h,k)+c*matrix2(e,f,h,i);
return det;
}

Thế là bạn đã có một máy tính giải hệ phương trình có độ chính xác không kém các máy tính cầm tay thông thường rồi. Sau đây là video kết quả