ksp gửi vào
- 42990 lượt xem
Có bao giờ bạn tự hỏi: "Dự án của mình làm tốt thế này, chạy ngon lành rành rành thế này, chắc không có bugs đâu?". Thực sự, nếu dự án của bạn không có phần xử lý số thực chấm động trong đó thì mình nghĩ phần code của bạn sẽ hoạt động ngon lành theo thời gian. Nhưng mà có số thực thì từ từ, chúng ta cần xét lại code. Trước đây, có một số bạn nhắn tin riêng hỏi mình về code với điểm chung là "code mình chạy ngon lành lúc đầu, sau đó bị lỗi, không rõ nguyên nhân". Loại trừ các phần code logic sai ra, thì hầu hết đều là do lỗi khi xử lý số chấm động mà không quan tâm đến nền tảng lập trình bên dưới! Mà cũng đúng, chúng ta rất dễ bị đánh lừa bởi chính đoạn code chúng ta viết. Vì nó có báo lỗi biên dịch đâu mà, kaka. Qua bài viết này, mình muốn phân tích và cùng các bạn rút kinh nghiệm về số chấm động float, cách hạn chế lỗi sai với số chấm động.
Vì sao tớ lại viết bài này?
Đây là một bài tập về nhà môn Phân tích độ phức tạp thuật toán, mình thấy rất hay và cũng liên quan đến các vấn đề mà mình từng gặp phải trong quá khứ và nhiều bạn cũng bị vấn đề này. Vì vậy, để tránh tình trạng lặp đi lặp lại một vấn đề và đóng góp một tài liệu tham khảo, mình viết bài này để cùng chia sẻ đến các bạn về "Vấn đề của số chấm động và số nguyên trong ngôn ngữ lập trình C++ trên board mạch Arduino".
Để dễ theo dõi, mình xin nêu lại bài toán:
Đề bài: Thực hiện phép nhân n * x. (n - nguyên; x - thực chấm động)!
- Khảo sát xem phép tính trên có luôn đúng khi kết quả chưa overflow hay không?
- Về mặt toán học, có thể thay n * x bởi : x + x + ... + x (n phép cộng).
- Khảo sát các kết quả đúng khi thay bằng phép cộng mà nhân n * x bị sai [Dùng thuật toán O(n)].
- Cải tiến để đề xuất và chạy thử thuật toán n * x có độ phức tạp O(log2n).
Số thực chấm động là gì?
Trước tiên, chúng ta CẦN PHẢI HIỂU rằng, máy tính chúng ta không thể lưu trữ số thực. Nó chỉ lưu trữ được số thực chấm chấm động. Vậy vì sao máy tính không lưu trữ được số thực? Khái niệm số thực chấm động là gì? Vì sao máy tính lại sử dụng nó để tính toán số thực trong máy tính.
Thực tế, số thực có hai phân loại: số vô tỉ và số hữu tỉ. Số vô tỉ là số không thể được biểu diễn dưới dạng tỉ số giữa 2 số nguyên, ví dụ như số π (số Pi). Vậy nên chúng ta cũng hiểu là với một máy tính hữu hạn chúng ta không thể nào biểu diễn được số thực nhánh số vô tỉ rồi! Thế còn số thực hữu tỉ thì sao? Ví dụ:
1412.669669669669669669669669669669669669669669669669669669
Đó thực sự là một số có giá trị không quá lớn nhưng vấn đề của nó chính là cái phần thập phân lên đến hàng chục số!?! Vì sao máy tính không lưu được cái mớ đó vào mà xử lý?
Cùng theo dòng lịch sử
Máy tính thời đầu, các máy tính sử dụng hệ cơ số 10 và bóng đèn chân không (nôm na lúc đó chưa có transitor nên chơi bóng này để tính toán á). Vậy nếu muốn lưu số trên vào máy tính này, chúng ta chỉ việc bật tắt số lượng đèn là được. Nhưng từ từ, giá của một cái bóng đèn chân không là bao nhiêu tiền? Đó là hàng đơn vị đến hàng chục đô la Mỹ thời đó (thế kỷ XX). Vậy nếu chỉ để lưu trữ cái số đó thôi chưa kể việc tính toán thì ta cũng thấy hơi bị tốn rồi đúng không nào. Và bản chất của các tư bản là không đầu tư vào những thứ không sinh lời, nghĩa là bạn chẳng cần quan tâm đến hàng chục chữ số kia, vốn dĩ nó vô nghĩa.
Kết thúc hệ máy tính thứ 1 (1945 - 1956), hai nhà khoa học Hoa Kỳ Jack Kilby và Robert Noyce đã phát minh ra IC, chính thức mở ra kỷ nguyên của thế giới máy tính điện tử mới! Đó là kết quả của "Quy luật thống nhất và đấu tranh của các mặt đối lập" (triết học Mác - Lênin). Cụ thể: Bóng chân không đã chuyển mình lên thành transistor, hệ 10 đã chuyển xuống còn hệ 2,... ngoài ra cái vụ lập trình chuyển từ việc đục lỗ sang lập trình bậc cao (chương trình nhúng). Từ đó đặt tiền đề cho các hệ máy tính thứ 3, 4 sau này.
Các bạn thấy đấy, máy tính thời nay qua quá trình biến đổi lịch sử để thích nghi với thời đại cùng giá thành rẻ để bạn có thể sở hữu để đọc bài viết này. Vì vậy, việc tiến hóa từ hệ 10 lên thành hệ 2 đã giúp chúng ta tiết kiệm chi phí tính toán và sản xuất. Nhưng vấn đè ở chỗ, với hệ 2 này, chúng ta phải chấp nhận một sự thật, đó là máy tính của chúng ta không thể nào lưu được chính xác đến 10 chữ số thực phân hư hồi hệ 10 với máy tính ENIAC hay UNIVAC. Nhưng, chúng ta có thể xấp xỉ nó với độ chính xác lớn đến từ 5 - 6 chữ số thập phân, một tỉ lệ hoàn toàn tối ưu trong việc phóng tàu vũ trụ  . Qua đó, mình muốn truyền đạt, số thực chấm động chính là kết quả của quá trình xấp xỉ giữa cái thực tế cần với cái lý thuyết cần. Một bên thực tế khoa học chỉ cần đúng một cách tương đối và chấp nhận sai số, còn một bên là thích cái tuyệt đối (truyền thống thôi nha, chứ các nhà xác suất thống kê thì tương đối sai số vẫn ok hehe). Ví dụ như: chúng ta tính toán số Pi thì chơi 3.14 là được òi, kết quả chấp nhận được, còn nhà toán học thích sự tuyệt đối nên dành thời gian viết chương trình máy tính để tính ra đến hàng ngàn, chục ngàn, trăm ngàn, triệu chữ số thập phân của số Pi. Chắc chắn thực tế người ta không cần chính xác đến thế nhưng qua đó chúng ta có thể thấy, nếu muốn chính xác ta hoàn toàn có thể làm được, với tốc độ rất nhanh (mạng siêu máy tính).
. Qua đó, mình muốn truyền đạt, số thực chấm động chính là kết quả của quá trình xấp xỉ giữa cái thực tế cần với cái lý thuyết cần. Một bên thực tế khoa học chỉ cần đúng một cách tương đối và chấp nhận sai số, còn một bên là thích cái tuyệt đối (truyền thống thôi nha, chứ các nhà xác suất thống kê thì tương đối sai số vẫn ok hehe). Ví dụ như: chúng ta tính toán số Pi thì chơi 3.14 là được òi, kết quả chấp nhận được, còn nhà toán học thích sự tuyệt đối nên dành thời gian viết chương trình máy tính để tính ra đến hàng ngàn, chục ngàn, trăm ngàn, triệu chữ số thập phân của số Pi. Chắc chắn thực tế người ta không cần chính xác đến thế nhưng qua đó chúng ta có thể thấy, nếu muốn chính xác ta hoàn toàn có thể làm được, với tốc độ rất nhanh (mạng siêu máy tính).
Vậy máy tính lưu trữ số chấm động như thế nào?
Mình sẽ không nói chi tiết vì mình thấy nó lý thuyết quá và theo mình thấy không cần hiểu cặn cẽ như thế để hiểu được các phần tiếp theo của mình. Nhưng nếu thích bạn hoàn toàn có thể đọc ở đây.
Số chấm động trong máy tính được hỗ trợ sẵn theo chuẩn IEEE754, trong đó có 2 loại: số chấm động có độ chính xác đơn (float), số chấm động có độ chính xác kép (double).
Nôm na, float có thể biểu diễn được từ 6-7 chữ số nghĩa sau phần thập phân, double thì có thể chơi được gấp đôi từ 12-14 số có nghĩa.
Thế máy tính biểu diễn những số thực chấm động này như thế nào?
Mình sẽ ví dụ về kiểu float, kiểu double tương tự nhưng tăng gấp đôi lên nha
.
Số thực dấu phẩy động được dùng để biểu diễn các số thực trong tính toán khoa học. Tổng quát một số thực X được biểu diễn theo kiểu số dấu phẩy động như sau: X = M*Re.
Trong đó:
- M là phần định trị (Mantissa)
- R là cơ số (Radix)
- E là phần mũ (Exponent)
Chuẩn IEEE754/85
- Cơ số R = 2
- Các dạng 32, 44, 64, 80 bít
Ví dụ dạng 32 bit
| 1 bít | 8 bít | 23 bít |
|---|---|---|
| S | e | m |
- S là bít dấu (số dương S = 0)
- e là mã excess của phần mũ E (e = E+127 hay E = e-127, số 127 ở đây là độ lệch bias)
- m là phần lẽ của phần định trị M (M = 1.m)
Do vậy công thức xác định giá trị số thực như sau: X = (-1)S * 1.m * 2e-127
Như vậy, một số float được gọi là không bị overflow nếu nó có thể biểu diễn thành dạng M*Re mà không còn phần nào "dôi ra" sau tính toán.
Khảo sát xem phép tính n*x (n - nguyên; x - thực chấm động) có luôn đúng khi kết quả chưa overflow hay không?
Từ câu hỏi, ta phân tích:
n: nguyên => ta chọn int để khảo sát
x: thực chấm động => ta chọn float để khảo sát.
Đề không nói rõ là x có bị overflow hay không bị overflow. Thành ra chúng ta sẽ chia trường hợp để khảo sát.
Ngoài ra, kết quả phép tính là không bị overflow, nghĩa là phép tính không vượt qua khả năng biểu diễn của float (-3.4028235E+38 đến 3.4028235E+38).
x không bị overflow
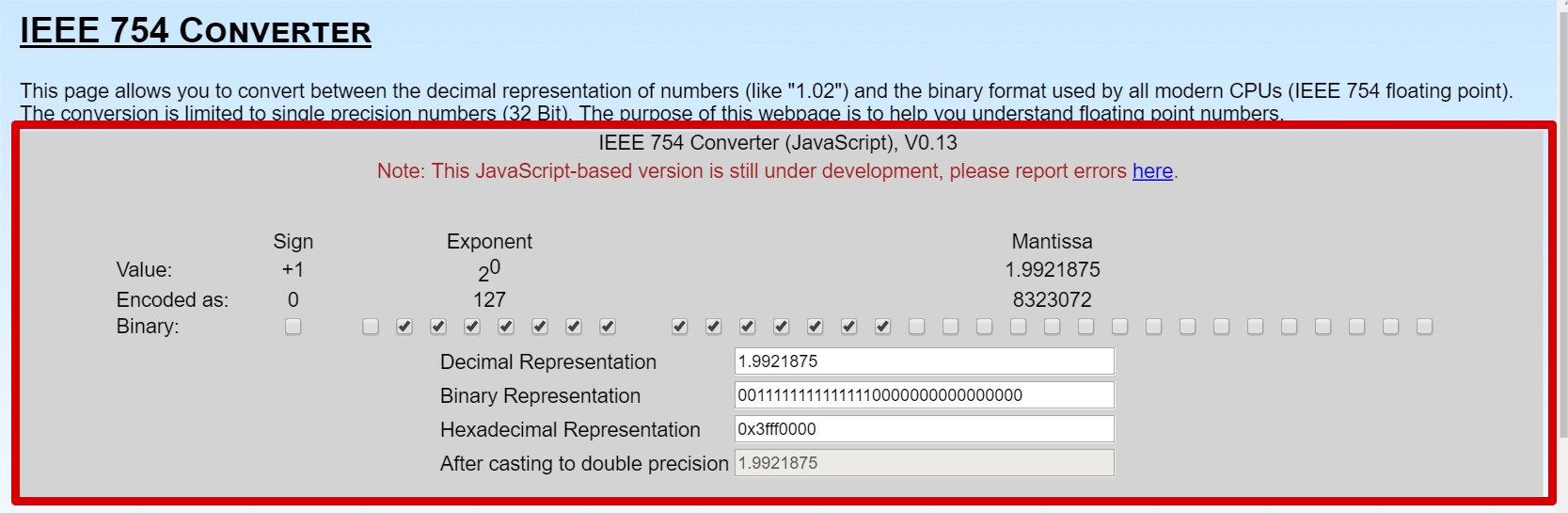
Chọn n = 6969; x = 1.9921875 (mình tạo số này ở https://www.h-schmidt.net/FloatConverter/IEEE754.html)
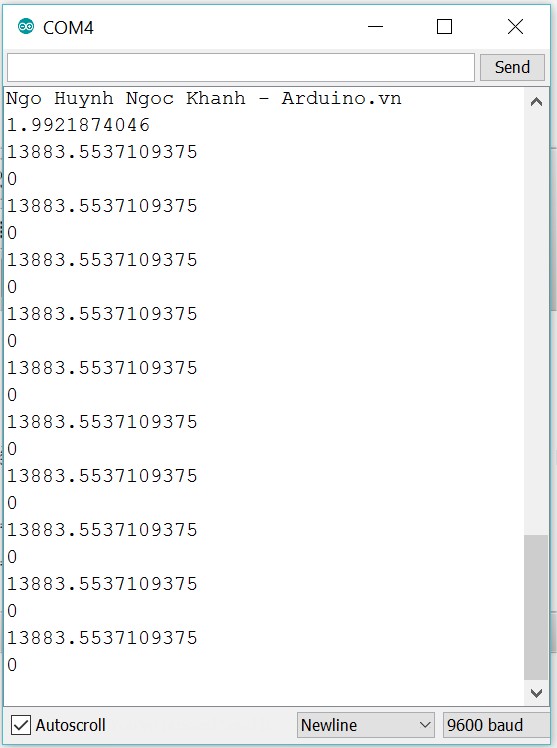
Kết quả được dự toán trên google là 13883.5546875
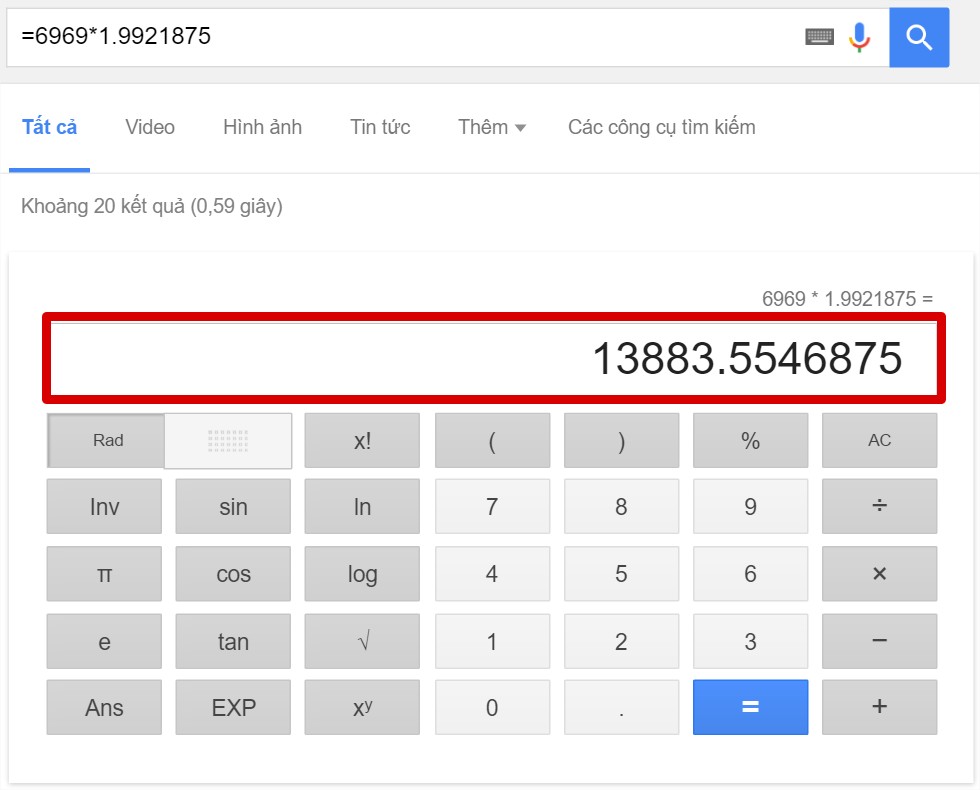
Và kết quả trên Arduino là hoàn toàn đúng với kết quả của google.
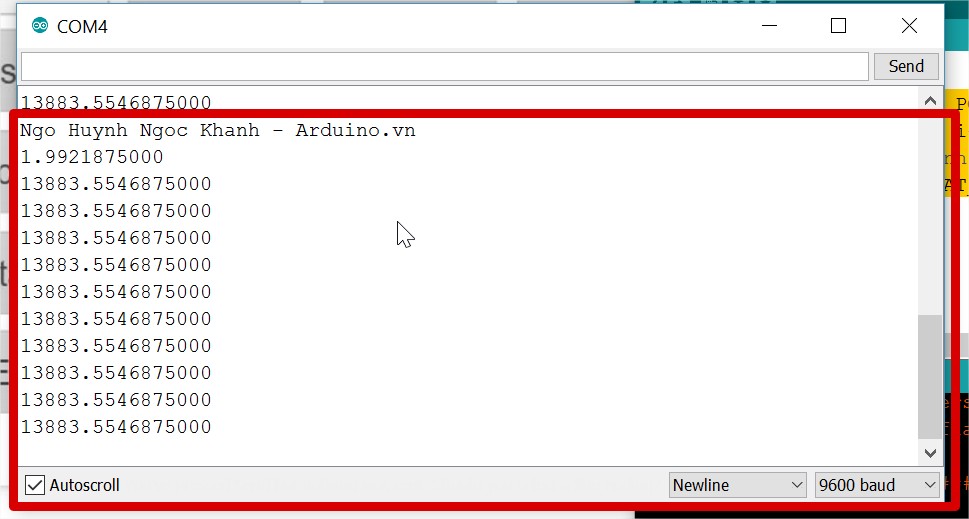
Mình cũng đã thử với rất nhiều n và x khác (miễn x nó có phần thập phân có nghĩa bé hơn 6-7 là ok - float; bé hơn 12 - 14 với double). Các bạn hoàn toàn có thể tự xây dựng lại thí nghiệm với đoạn code sau.
#define FLOAT_POINT_SIZE 10
void setup() {
Serial.begin(9600);//Mở serial ở baudrate 9600
Serial.println("Ngo Huynh Ngoc Khanh - Arduino.vn"); //Xem như mở đầu ahihi
int n = 6969; //số n
float x = 1.9921875; //số x
//lặp 10 lần
Serial.println(x, FLOAT_POINT_SIZE);
for (int i = 0; i < 10; i++) {
float y = n * x; //tính y
Serial.println(y, FLOAT_POINT_SIZE); //in kết quả ra màn hình
}
}
void loop(){}x bị overflow
Mình thay x thành 1.9921874 (sửa số 5 từ số 1.9921875 ở trên thành số 4 thôi mà  ).
).
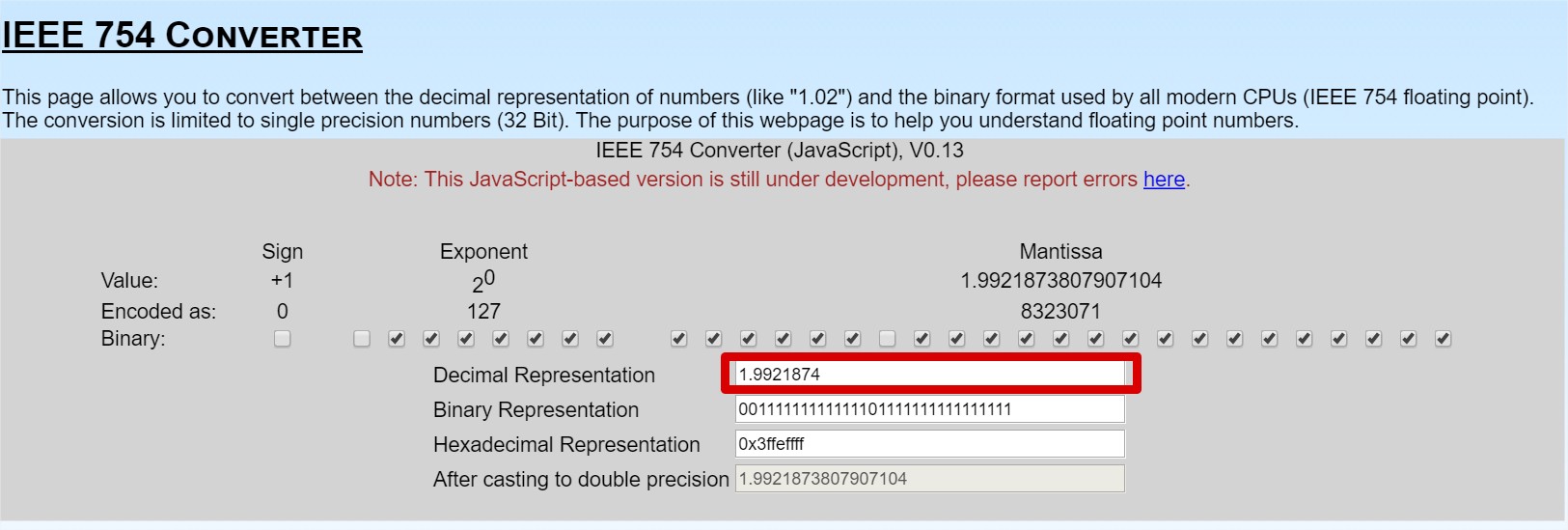 Như ta thấy ở phần "After casting to double precision" với 16 số có nghĩa, ta thấy con số 1.921874 không hề được biểu diễn đúng giá trị thực trên máy tính.
Như ta thấy ở phần "After casting to double precision" với 16 số có nghĩa, ta thấy con số 1.921874 không hề được biểu diễn đúng giá trị thực trên máy tính.
Kết quả dự tính ở thế giới thật (google) là 13883.5539906. Nhưng bé Arduino nhà ta lại ra 13883.5537109375, chỉnh float y thành double y thì nó cũng thế nhưng dài ra nữa. Như vậy, ta đã thấy được sự sai số và khẳng định có tồn tại sự sai số trên Arduino khi tính toán số chấm động. Thật bất ngờ phải không nào?
Kết luận ở câu hỏi này
Không phải lúc nào cũng có chuyện nhân x với n nó luôn đúng, nó chỉ đúng nếu x có thể biểu diễn dưới dạng M*Re với sai số (dư) là 0. Còn lại thì lỗi tè le!
Khảo sát các kết quả đúng khi thay bằng phép cộng mà nhân n * x bị sai [Dùng thuật toán lặp].
Mình sẽ khảo sát về thời gian và kết quả nhé. Xem nó chạy tốn bao nhiêu mi li giây.
Hai số n và x lần lượt là:
int n = 6969; //số n float x = 1.9921874; //số x
#define FLOAT_POINT_SIZE 10
void setup() {
Serial.begin(9600);//Mở serial ở baudrate 9600
Serial.println("Ngo Huynh Ngoc Khanh - Arduino.vn"); //Xem như mở đầu ahihi
int n = 6969; //số n
float x = 1.9921874; //số x
//lặp 10 lần
Serial.println(x, FLOAT_POINT_SIZE);
for (int i = 0; i < 10; i++) {
float y = 0; //tính y
unsigned long start = millis();
for (int j = 0; j < n; j++)
y += x;
unsigned long finish = millis();
Serial.println(y, FLOAT_POINT_SIZE); //in kết quả ra màn hình
unsigned long duration = finish - start;
Serial.println(duration);
}
}
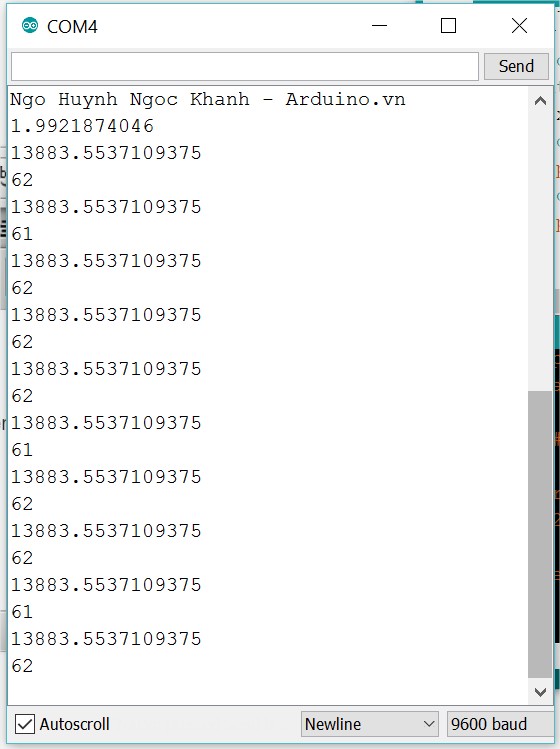
void loop(){}Theo như kết quả trên con promini của mình thì nó cần đến 61ms để thực hiện được một phép nhân mà kết quả cho ra cũng không khác gì so với phép * truyền thống (cần ít hơn 1ms).
|
Truyền thống (*)
|
Cải tiến (vòng lặp O(n))
|
Kết luận cho câu hỏi
Kết quả không khá hơn mà còn chậm hơn nhiều so với thực tế.
Cải tiến để đề xuất và chạy thử thuật toán n * x có độ phức tạp O(log2n)
#define FLOAT_POINT_SIZE 10
float mul(int n, float x) {
if (n == 1)
return x;
int m = n / 2;
float y = mul(m, x);
if (n % 2 == 0) {//n chẵn
return y + y;
} else { // n lẻ
return y + y + x;
}
}
void setup() {
Serial.begin(9600);//Mở serial ở baudrate 9600
Serial.println("Ngo Huynh Ngoc Khanh - Arduino.vn"); //Xem như mở đầu ahihi
int n = 6969; //số n
float x = 1.9921874f; //số x
//lặp 10 lần
Serial.println(x, FLOAT_POINT_SIZE);
for (int i = 0; i < 10; i++) {
float y = 0; //tính y
unsigned long start = millis();
y = mul(n, x);
unsigned long finish = millis();
Serial.println(y, FLOAT_POINT_SIZE); //in kết quả ra màn hình
unsigned long duration = finish - start;
Serial.println(duration);
}
}
void loop(){}Ý nghĩa thuật toán như sau:
y = x + x + .... + x (n lần x)
Như vậy, mình sẽ viết thành:
- Nếu n = 1
- y = x
- Nếu n chẵn
- y = y' + y' (với y' = m * x, trong đó m = n / 2)
- Nếu n lẻ
- y = y' + y' + x (với y' = m * x, trong đó m = n / 2)
Sau khi kiểm nghiệm thực tế, thì tốc độ chạy của hàm trên rất nhanh, cho kết quả trong chưa đến 1ms với sai số giống hệt phép * thông thường.
Kết luận
Thuật toán O(1) ở phép nhân 2 số thực cũng không chạy nhanh hơn mấy so với thuật toán O(log2(n)) như trên. Kết luận, chúng ta không được xem độ phức tạp O(1) là nhanh hơn O(log2(n)) trong khi lý theo lý thuyết độ phức tạp phép * được xem là O(1) thì nhỏ thua hơn O(log2(n)) và thường thì các phép tính có độ phức tạp O(1) sẽ nhanh hơn O(log2(n)).
Kết luận
Vậy kinh nghiệm rút ra là gì?
Một khi thực hiện các phép nhân n * x thì các bạn phải lựa chọn x không bị overflow để tránh tình trạng sai số và đúng tuyệt đối. Còn đối với các trường hợp còn lại chắc chắn là sai số vì đó là bản chất rồi! Còn đối với các trường hợp m * n * x hay các công thức phức tạp hơn đều có thể quy về m * n * x thì chúng ta xử lý nó như thế nào? Chờ đợi bài viết sau của mình nhé!