quocbao gửi vào
- 199622 lượt xem
Định nghĩa
Bit là các chữ số (trạng thái) “0” và “1”. Một chuỗi các bit ghép lại sẽ cho ta một dãy các số 0 1 mà hệ tính toán trên những con số này được gọi là hệ nhị phân. Khi nhắc tới bit math (toán bit) tức là nhắc tới việc tính toán trong hệ số này.
Chuyển đổi hệ thập phân - nhị phân
Quy ước: một số nhị phân khi được biểu diễn phải có tiền tố “0B” đứng ở đầu, sau đó là dãy các bit 0 1. Trong so sánh (lớn hơn, bé hơn, bằng), 0 được xem như là giá trị sai (false) và 1 là giá trị đúng (true).
Ví dụ: A = 0B10111001. Trong đó A gồm có 8 bit từ bit 0 đến bit 7 được đánh số từ phải sang trái.

Gọi B là dạng thập phân của A thì:
B = 27 x 1 + 26 x 0 + 25 x 1 + 24 x 1 + 23 x 1 + 22 x 0 + 21 x 0 + 20 x 1 = 185

Chú ý: một số cho dù có được biểu thị ở dạng nhị phân, thập phân hay bất kì dạng nào khác đi chăng nữa thì đều có giá trị như nhau.
Các phép toán thao tác trên hệ nhị phân
Nếu trong hệ thập phân ta có các phép toán như cộng, trừ, nhân, chia,… thì trong hệ nhị phân chúng ta có các phép toán and, or, xor, not, dịch trái (bits shift left) và dịch phải (bits shift right).
1/ AND (&)
Giả sử ta có 2 bit 0 và 1 thì:
0 and 0 = 0 1 and 1 = 1 0 and 1 = 0 1 and 0 = 0
Như vậy chỉ khi nào 2 bit đều là 1 thì kết quả trả về mới là 1, các trường hợp còn lại đều là 0.
Phát biểu bằng lời: nếu cả 2 điều kiện cùng đúng thì kết quả là đúng, và dĩ nhiên những trường hợp còn lại là sai.
Ví dụ
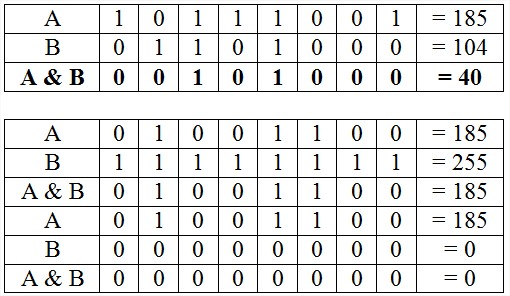
2/ OR ( | )
Giả sử ta có 2 bit 0 và 1 thì:
0 or 0 = 0 1 or 1 = 1 0 or 1 = 1 1 or 0 = 1
Như vậy chỉ cần 1 trong 2 bit là 1 thì kết quả trả về sẽ là 1.
Phát biểu bằng lời: nếu có một trong 2 điều kiện là đúng thì kết quả là đúng
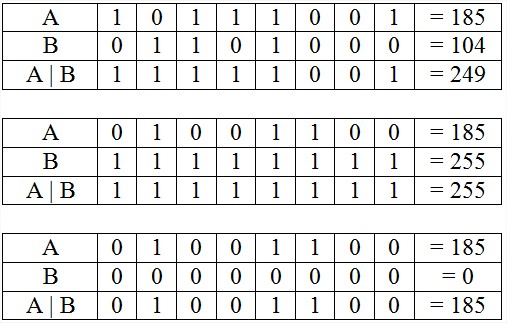
3/ XOR (^)
Giả sử ta có 2 bit 0 và 1 thì:
0 xor 0 = 0 1 xor 1 = 0 0 xor 1 = 1 1 xor 0 = 1
Như vậy nếu 2 bit khác nhau sẽ cho ra kết quả 1 và ngược lại, 2 bit giống nhau sẽ cho ra kết quả 0. Từ đó ta thấy nếu A xor B = 0 thì A = B
Phát biểu bằng lời: nếu 2 điều kiện mang giá trị đúng – sai khác nhau thì kết quả trả về là đúng.
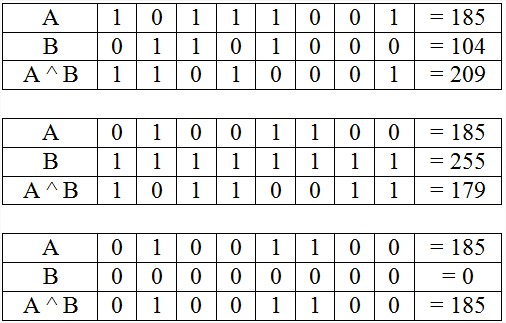
4/ NOT (~)
Phép toán not thay đổi bit 0 thành bit 1 và ngược lại, bit 1 thành bit 0.
Tức là:
not 0 = 1 not 1 = 0
Phép toán này còn được gọi là phép đảo bit.
Ví dụ:
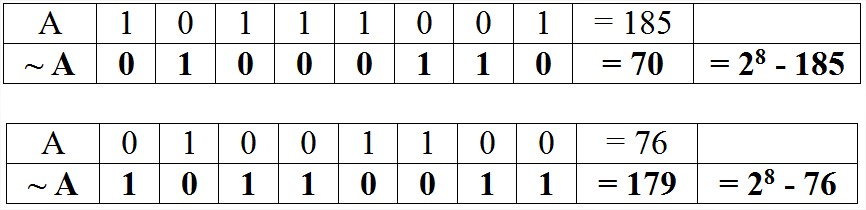
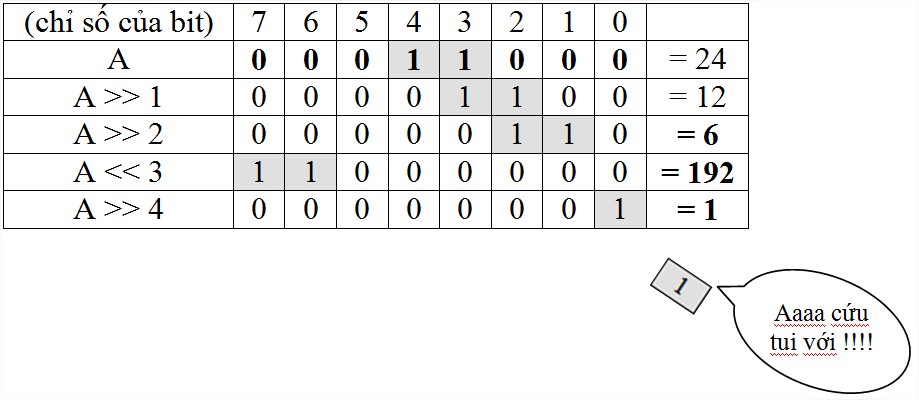
5/ Dịch trái – Bits shift left ( << ) và Dịch phải – Bits shift right ( >> )
- Phép dịch trái hay dịch phải được gọi chung là phép dịch bit.
- Khi dịch một dãy bit A được đánh số từ bit 0 đến bit n, chỉ số của các bit sẽ thay đổi còn giá trị của mỗi bit sẽ vẫn giữ nguyên. Như vậy giá trị của A sẽ thay đổi
- Khi dịch dãy bit A sang phải n đơn vị tức là chỉ số của mỗi bit trong A sẽ bị trừ đi n đơn vị. Ngược lại, khi dịch sang trái n đơn vị tức là chỉ số của mỗi bit sẽ được cộng thêm n đơn vị
- Sau khi dịch bit, các bit có chỉ số âm sẽ bị bỏ đi.
Ví dụ
Khi bạn dịch một chuỗi bit x sang phải y bit mà bit cao nhất trong x là "1", bạn có thể gặp phải một số sự cố không mong muốn. Điều này còn tùy vào việc bạn lưu trữ x trong một biến với kiểu dữ liệu là gì.
Trong lập trình Arduino, giả sử ta có đoạn chương trình sau:
void setup() { Serial.begin(9600); int x = 65526; //x = 0B1111111111110000 int y = x >> 3; Serial.println(y); Serial.println(y,BIN); } void loop() { }Nếu thử tính thủ công, bạn sẽ cho rằg y = 0B0001111111111110, tức y = 8190. Tuy nhiên thực tế, bạn lại nhận được y = -2 ở dạng số nguyên và "11111111111111111111111111111110" ở dạng bit. Điều này là không đúng.
Người ta gọi hiện tượng này là "sign extension". Lí do phát sinh ra nó được người ta mô tả là "esoteric historical" (tạm dịch: "bí ẩn lịch sử").
Để khắc phục hiện tượng này, bạn phải khai báo biến x ở kiểu "unsigned int". Hãy thử lại để kiểm tra nhé



