Hiện tượng tràn số trong lập trình C trong Arduino

Số nguyên là gì? Số nguyên được định nghĩa là tập các số {1, 2, 3,…}, các số đối của nó {-1, -2, -3,…} và số không. Trên máy tính, số nguyên được lưu trữ bởi các kiểu dữ liệu là byte, int, unsigned int, long, unsigned long,… bằng những bit 0 và 1. Trong bài này, chúng chỉ nói về kiểu int và unsigned int, vì những kiểu khác (như long, unsigned long, byte, smallint,…) đều có cách thức tương tự.

Trong ngôn ngữ lập trình C (Arduino), ta có thể xem một kiểu dữ liệu số nguyên là một vòng tròn chứa các số trong khả năng biểu diễn của nó, mà trong đó int có khả năng biểu diễn các số từ -32,768 đến 32,767 (-2¹⁵ đến 2¹⁵-1) (16 bit) và unsigned int có khả năng biểu diễn các số từ 0 đến 65535 (0 đến 2¹⁶ - 1). Như vậy, mỗi kiểu dữ liệu sẽ được xem là một bản quay số của một chiếc điện thoại bàn quay số thời thập niên 80!

Như hình trên, mỗi khi ta thực hiện một phép cộng x đơn vị vào một biến số nguyên, có nghĩa là ta đẩy vòng tròn số đó về bên trái đi x lần (mỗi lần một số) và việc thực hiện phép trừ x đơn vị cũng chính là việc đẩy vòng tròn đó qua phải x lần.

Xét đoạn mã nguồn C trong Arduino như sau:

void setup() {
  
  Serial.begin(9600); // Mở cổng Serial ở mức baudrate 9600
  
  unsigned int a = 200, b = 201;
  double x, y;
  
  x = a - b + 108.0;
  y = a - b + 108; 
  
  Serial.println(x);
  Serial.println(y);
}

void loop() {
  // do nothing ^_^
}

Khi biên dịch và chạy chương trình, ta sẽ được kết quả trả về như sau:

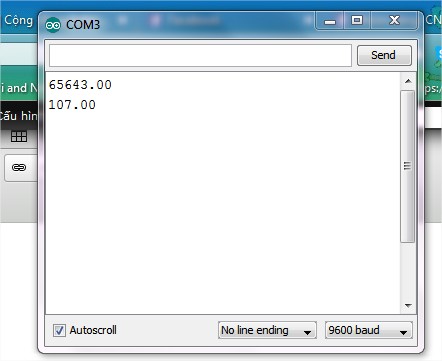
Như vậy, ta nhận thấy sự vô lý (theo lý thuyết toán học tự nhiên) ở giá trị trả về của biến x. Theo toán học, đáng nhẽ ra giá trị x phải bằng giá trị y. Nhưng trong trường hợp đoạn mã trên, đã có một điều gì đó xảy đến với x? và điều đó đã biến x lớn hơn y đến khoảng 613 lần!

Tại sao lại có kết quả quả như vậy, tràn số là gì, và lý do của việc tràn số?

Ta đã mắt lỗi một lỗi khá lớn trong việc lập trình, đó là việc chỉ tư duy theo kiểu toán học tự nhiên, mà không suy nghĩ đến các cơ sở của việc lập trình (đã nói ở trên). Dẫn đến việc nghĩ máy tính hoạt động sai.

Ở trên, ta đã biết về cách biểu diễn số nguyên trong C, thực chất là một vòng tròn (giống như chiếc bàn quay của điện thoại bàn thập kĩ 80 hay là mô hình chiếc nón kì diệu) trong ngôn ngữ tự nhiên. Như vậy, nếu ta quay vòng tròn đó từ vị trí hiện tại đến giới các giới hạn có thể biểu diễn của nó thì nó cứ tiếp tục quay cho đến khi đủ số vòng thì thôi. Để dễ hiểu, chúng ta cùng xét hình sau:

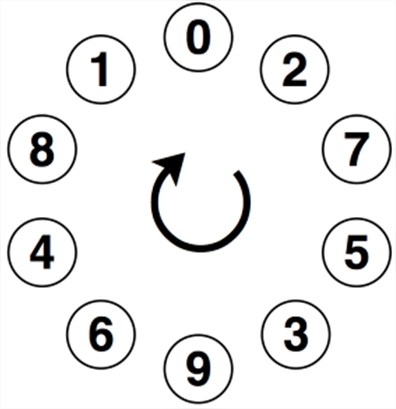
Ta đang đứng ở số 0 và đi sang phải 11 bước thì lúc này ta sẽ đứng ở vị trí số ô 2. Và nếu đi thêm 1 bước nữa ta sẽ ở ô số 7.

Xét lại lỗi đã xảy ra ở đoạn mã nguồn trên, chúng ta thấy rằng, a và b đều là một nguyên không âm (unsigned int). Trong đó, a mang giá trị 200, còn b mang giá trị 201. Nếu xét trên mặt toán học tự nhiên, thì kết quả của biểu thức: a – b + 108.0 = -1 + 108 = 107. Số -1 và 108 ở đâu mà ra? Theo toán học tự nhiên thì 200 – 201 = -1 ⇒ a – b có kết quả là -1 ⇒ -1 là kết quả của phép toán a – b, còn 108.0 có phần thực là 0 ⇒ 108.0 = 108 ⇒ 108 = 108.0. Trong khi đó, máy tính lại hiểu theo một hướng khác – theo hướng kiểu dữ liệu. Xét lại biểu thức trên, máy tính sẽ thực hiện các phép toán theo thứ tự ưu tiên đúng như trong đại số tự nhiên, như vậy, phép toán a – b sẽ được thực hiện trước, sau đó sẽ lấy kết quả đó cộng với 108.0. Trong lập trình nói chung và ngôn ngữ C nói riêng, có một điểm khác cơ bản với đại số tự nhiên, đó là khái niệm kiểu dữ liệu. Nghĩa là phép toán nào thực hiện trước thì sẽ dùng kiểu dữ liệu có kích thước lớn nhất giữa hai phần tử để lưu trữ kết quả của phép toán đó. Xét lại ví dụ trên, ta thấy a và b đều mang kiểu unsigned int ⇒ a – b cũng sẽ mang kiểu unsigned int ⇒ a – b không thể nào bằng -1 vì kiểu dữ liệu unsigned long không thể hiện giá trị đó!

Vậy a – b thể hiện một số bao nhiêu? Cùng nhớ lại định nghĩa và xét lại những gì ta có, a = 200 và b = 201. Hãy tưởng tượng có một mãnh giấy dài hình chữ nhật (có cạnh nhỏ = 1, cạnh lớn = 2¹⁶ – 1) ghi các số từ 0 đến 2¹⁶ – 1 ( = 65535), mỗi số ghi trong 1 ô hình vuông có kích thước 1x1, bây giờ ta sẽ dính mép của ô số 0 với mép của ô số 2³² – 1 lại với nhau để tạo thành một vòng tròn số, giả định ta đứng ở ô số 200 và đi về bên trái vòng tròn 201 ô. Khi đi xong được 200 bước, ta sẽ đứng ở ô số 0 và khi bước thêm một bước nữa ta sẽ đứng ở ô 2¹⁶ – 1, đúng không? Đó, cái này chính là sự tràn số, tràn số là gì? Tràn số là việc kết quả của một phép tính chạy vượt qua khả năng lưu trữ của kiểu dữ liệu và lúc này nó sẽ đội lên giá trị cao nhất hoặc thấp nhất mà kiểu dữ liệu đó có thể biểu diễn. Cứ nghĩ đơn giản khi bạn đi trên vòng tròn số, khi bạn đi tới ranh giới dính bằng băng keo, thì bạn chỉ việc bước qua cho đến khi bạn phải dừng lại.

Tóm lại, khi thực hiện xong phép tính a – b, ta sẽ được giá trị là 2¹⁶ – 1, sau đó chỉ việc lấy số đó cộng thêm với 108.0 ta sẽ được một giá trị như đầu bài với kiểu dữ liệu là double. Vì 108.0 là kiểu double (mặc định các hằng số thực khi chưa khai báo kiểu dữ liệu trong C là kiểu double).

Bây giờ, ta sẽ xét thêm một tí xíu về biểu thức y = a – b + 108, tại sao biểu thức này lại trả về được số 107.0, đúng bằng kết quả của “tự nhiên” chủ nghĩa?

Đầu tiên, chúng ta có thể xác định được ngay số 108 mang kiểu int (singed – có dấu). Vấn đề ở đây nằm ở chỗ, một kiểu số unsigned int khi cộng với một số kiểu int sẽ là kiểu số gì và cộng như thế nào?

Như đã nói ở trên, a – b sẽ cho ra giá trị 2¹⁶ – 1 sau khi bị tràn số. Trong C, bất kì kiểu có dấu nào cũng dùng 1 bit bên phải nhất để lưu trữ dấu cho một số. Số 1 là dấu -, và số 0 là dấu +. Như vậy, kiểu int chỉ có 15 bit là lưu trữ phần nguyên của một số, nên số 108 sẽ bị ép thành kiểu unsigned int trước khi cộng với (a – b). Việc ép kiểu thực chất là chương trình sau khi dịch sẽ không xem bit 1 ở đầu để lưu dấu nữa mà xem nó như 15 bit còn lại. Kết quả chúng ta sẽ nhận được là 2¹⁶ – 1 + 108 = 2¹⁶ + 107 ⇒ tràn số thành 107. ⁽¹⁾

Nếu điều ⁽¹⁾ đúng thì kết quả của phép tính (a – b) – 1 = (a – b) + (-1) = 2¹⁶ – 1 + 2¹⁶ – 1 = 2¹⁶ – 2. Và qua thực nghiệm chương trình đã chứng minh điều đó!

void setup() {
  
  Serial.begin(9600); // Mở cổng Serial ở mức baudrate 9600
  
  unsigned int a = 200, b = 201;
    
  //Thể hiện bit của số (a - b) - 1
  Serial.println((a - b) - 1);
  Serial.println((a - b) - 1, BIN);
  
  //Thể hiện bit của số (a - b) + (-1)
  Serial.println((a - b) + (-1));
  Serial.println((a - b) + (-1), BIN);
}

void loop() {
  // do nothing ^_^
}

Làm thế nào để khắc phục tình trạng tràng số, và những lợi ích từ việc đó?

Tuy nhiên, trong tin học, cái cốt lõi vẫn là thực hiện các phép tính của toán học một cách chính xác và nhanh chóng nhất. Vậy với đoạn mã nguồn trên, chúng ta đã không đạt được cái cốt lõi ấy. Như vậy, vấn đề đặt ra là làm thế nào để khắc phục tình trạng tràn số.

Cùng xét lại các thông tin từ ví dụ, ta thấy, có phép trừ trong biểu thức. Theo toán học tự nhiên, khi c = a – b thì c >= 0 nếu a >= b và c < 0 nếu a < b. Trong ví dụ trên, thì a < b ⇒ c < 0 ⇒ tràn số. Như vậy, ta có thể rút ra một luật, khi có phép trừ trong biểu thức số học thì ta không nên dùng unsigned int (hay bất cứ kiểu dữ liệu nào có chữ unsigned) vì như vậy sẽ gây ra tình trạng tràng số. Trong ngôn ngữ pascal, sẽ không có khái niệm tràn số phức tạp như thế này, mà nó chỉ đơn giản là một “lỗi” khi biên dịch!

Ngoài ra, ta cần phải tính toán xem giới hạn tối thiểu và tối đa của biểu thức ta cần tính toán, từ đó lựa ra các kiểu dữ liệu phù hợp.

Việc khắc phục “bệnh” tràn số ở C (Arduino) rất quan trọng, vì điều đó sẽ giúp cho việc lập trình tốn ít thời gian cho việc debug các lỗi liên quan đến cấu trúc dữ liệu, tăng tính tin cậy của thuật toán,…!